From the statement, we know that:

If we extend the segments AD and BC, we have:
From the picture, we see that:
1) The angle m∠SBA is the complement angle of m∠ABC, so we have:
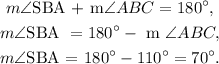
2) m∠SBA and m∠WAZ are congruent angles, so we have:
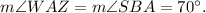
3) Finally because m∠WAZ and m∠BAD are opposite angles, they must be equal:
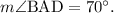
Answer
m∠BAD = 70°