Question

3. x-intercept 4, y-intercept 2, passes through Example Solution 22 - 202 +21 he given center and radius. (b) C(-2,-5), r = 4 (d) C(2, -3), r = 6 given properties. (0, 0) Center (5,-2), ² Plot the centes to the right, The center 5. Center on x = 3, radius 13, passes throw (6.5)

Answer 1

To solve we use the following expression:

`(x-h)^2+(y-k)^2=r^2`

Here (h, k) is the center of the circle, now we solve:

5. We calculate it as follows:

`(6-3)^2+(5-k)^2=13`

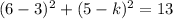
We have to solve now for k:

`\Rightarrow9+(k^2-10k+25)=13\Rightarrow k^2-10k+21=0`

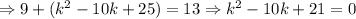
Now using the quadratic formula we solve:

`k=\frac{-(-10)\pm\sqrt[]{(-10)^2-4(1)(21)}}{2(1)}\Rightarrow\begin{cases}k=7 \\ k=3\end{cases}`

Now, we have to test each value of k as follows:

We replace the values of k and obtain the following equations:

`\begin{cases}(x-3)^2+(y-7)^2=13 \\ (x+3)^2+(y-3)^2=13\end{cases}`

Now, we test the point given (6, 5):

`\begin{cases}(6-3)^2+(5-7)^2=13 \\ (6-3)^2+(5-3)^2=13\end{cases}\Rightarrow\begin{cases}13=13 \\ 13=13\end{cases}`

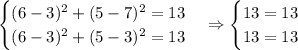
So, we will proceed as follows since both values are equivalent:

So, both equations represent a circle with radius sqrt(13), with a center at x = 3 and that passes the point (6, 5).

7. We calculate it as follows:

`(0-h)^2+(3-0)^2=25`

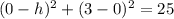
Now, we solve for one of the possible values:

`\Rightarrow h^2=16\Rightarrow h=\pm4`

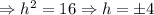
So, its center is located in either (4, 0= 0r (-4, 0), now we proceed as follows:

`\begin{cases}(x-4)^2+(y-0)^2=25 \\ (x+4)^2+(y+0)^2=25\end{cases}`

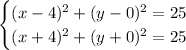
Now, we test the values: given the point (0, 3):

`\begin{cases}(0-4)^2+(3)^2=25 \\ (0+4)^2+(3)^2=25\end{cases}\Rightarrow\begin{cases}25=25 \\ 25=25\end{cases}`

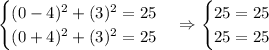
And we can also see the following graph:

This means, that any of the two equations describe the circle in the text.