Question

Please help with this word problem. Claire is using little wooden cubes with edge length 1/2 inch to build a larger cube that has edge length 4 inches. How many little cubes does she need? Explain your reasoning.

Answer 1

Step-by-step explanation:

The question we have to ask ourselves is "how many smaller cubes fit into the larger cube?".

The answer is found by dividing the volume of the larger cube by the volume of the smaller cube.

Now the volume of a cube is given by

`V=a^3`

where a = side length of the cube.

Now in the case of our smaller cubes, their side length is a = 1/2 in; therefore, the volume of one cube is

`V=((1)/(2)in)^3`
`V=(1)/(8)in^3`

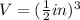
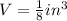
Now the side length of the larger cube is 4 in; therefore, its volume is

`V=(4in)^3`
`V=64in^3`

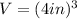
Now, how many smaller cubes fit into the larger cube?

To find the answer we see how many smaller cubes make the volume of the larger cube.

The answer is found by dividing the volume of the larger cube by the volume of the smaller cube.

`(64in^3)/(1/8in^3)=64*8=512`

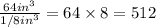
Hence, Claire needs smaller 512 cubes to build the larger cube.