Question

The population of a Midwestern city follows the exponential law. If the population decreased from 900,000 to 800,000 from 2008 to 2010, what will the population be in 2012?Use the equation N(t)= N0e^kt, wher N0 is the initial value, k being the constant that represents decay, and t being equal to time in years.Please use numbered sentences to explain your work!

Answer 1

Given

The population of the city follows an exponential law.

Population at 2008 = 900000

Population at 2010 = 800000

The population decrease follows an exponential decay law which is defined as:

`\begin{gathered} N(t)\text{ = N}_0e^(kt) \\ Where\text{ k is the decay rate} \\ N_0\text{ is the initial amount} \end{gathered}`

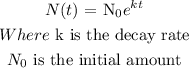
For the given problem:

`N_o\text{ = 900000}`

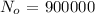
After 2 years (t =2), the population decreased to 800000. Hence we can write:

`\begin{gathered} 800000\text{ = 900000e}^(2k) \\ e^(2k)\text{ = }(800000)/(900000) \\ e^(2k)\text{ = }(8)/(9) \\ 2k\text{ = }\ln((8)/(9)) \\ k\text{ = -0.0589} \end{gathered}`

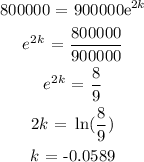
Hence, the equation the represents the population (N(t)) as a function of year (t):

`N(t)\text{ = 900000e}^(-0.0589t)`

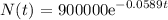
The population in 2012 is the population after 4 years ( t =4)

Substituting into the formula and solving:

`\begin{gathered} N(t=4)\text{ =900000e}^(-0.0589*4) \\ =\text{ 711086.9845} \\ \approx\text{ 711087} \end{gathered}`

Hence, the population in 2012 would be 711087