Hi, can you help me answer this question please, thank you

Question

asked Apr 21, 2023 72.9k views

1 Answer

Bobby Battista · Answer 1 · 2023-04-25T01:02:23+0000

Step-by-step explanation

We have that the mean is 95/500 = 0.19

Then, the standard error is as follows:

$SE=\sqrt[]{((0.19\cdot(1-0.19))/(500))}=0.017$

Now, the value of alpha is as follows:

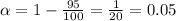
$\alpha=1-(95)/(100)=(1)/(20)=0.05$

The critical probability(p*) is as follows:

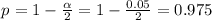
$p^{}=1-(\alpha)/(2)=1-(0.05)/(2)=0.975$

Now, we need to find the z-score by assuming a normal distribution, we can use the z-score table:

z=0.8340

Next, the margin of error is as follows:

ME = 0.8340 * 0.017 = 0.0142

The confidence interval is 0.19 + or - 0.0142

0.176 < p < 0.204