Given the following inequality:
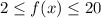
You know that:

Then, you need to rewrite the inequality as follows:

To solve the inequality, you can follow these steps:
1. Add 1 to all the three parts of the inequality:
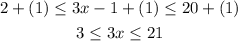
2. divide all the three parts of the inequality by 3:
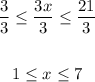
Notice that it can be expressed as a double inequality. This indicates that two inequalities are joined.
Then, to graph the solution on the Number Line, you need to follow the steps shown below:
1. Since both symbols are:
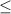
You can draw to draw a square bracket "[" on the number 1 and another square bracket "]" on the number 7.
2. Draw a line that connects or join the brackets.
Then, you get this graph:
Therefore, the answers are:
- Solution:
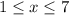
- Graph: Option A.