D. 100.5 cubic inches
Step-by-step explanation
Step 1
the volume of an oblique cone is given by:
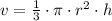
then, let
h=6
radius = unknown= r
Step 2
find the radius
we have a right triangle
where
hypotenuse(black)= 10
angle(yellow) =x
adjacent side(green)=6
opposite side = diameter(purple)
diameter = 2 * radius=opposite side
then,
radius(purple)=(diameter/2)
use the Pythagoras Theorem to find diameter
![\begin{gathered} P\mathrm{}T. \\ \text{opposite side}^2+adjacentside^2=hypotenuse^2 \\ \text{replace} \\ \text{diameter}^2+(6in)^2=(10in)^2 \\ isolate\text{ diameter} \\ diameter^2=(10in)^2-(6in)^2 \\ diameter^2=100in^2-36in^2 \\ diameter^2=64in^2 \\ \sqrt[]{diameter^2}=\sqrt[]{64in^2} \\ \text{diameter}=\text{ 8 inches} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ivq6u3luutw316daroaxcmg500ivfhd3vc.png)
so, diameter is 8 inches
Step 3
using the diameter, find the radius

Step 4
finally, replace the values for h and r in the volume formula
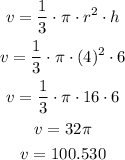
so, the answer is D. 100.5 cubic inches