Question

The height h in feet of a projectile launched vertically upward from the top of a 96-foot tall tower has an initialvelocity of 80 ft/sec.h=-16t^2+80t+96What is the maximum height of the projectile? | Select]How long did it take the projectile to reach its maximum height? Select]How long will it take the projectile to hit the ground? | Select]

Answer 1

Answe

Step-by-step explanation:

If we have an equation of a parabola with the form:

`y=ax^2+bx+c`

Where y and x are the variables and a, b, and c are constants, the x-coordinate of the vertex is calculated as:

`x=-(b)/(2a)`

In this case, the equation h=-16t^2+80t+96 is the equation of a parabola where h and t are the variables. So, the coordinates (t, h) where the projectile reaches the maximum height can be calculated as:

`t=-(b)/(2a)=-(80)/(2(-16))=-(80)/(-32)=2.5`

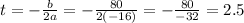
Because b is the number beside the t and a is the number beside t². Then, when t is 2.5 seconds the value of h is equal to:

`\begin{gathered} h=-16t^2+80t+96 \\ h=-16(2.5)^2+80(2.5)+96 \\ h=196ft \end{gathered}`

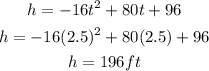
Therefore, the maximum height of the projectile is 196 ft and the projectile takes 2.5 seconds to reach this height.

On the other hand, the projectile will hit the ground when the value of h is equal to 0. So, we need to solve the following equation:

`\begin{gathered} h=-16t^2+80t+96 \\ 0=-16t^2+80t+96 \end{gathered}`

So, dividing by -16 and factorizing, we get that the values of t that satisfy the equation are:

`\begin{gathered} (0)/(-16)=(-16t^2+80t+96)/(-16) \\ 0=t^2-5t-6 \\ 0=(t-6)(t+1) \\ t-6=0\to t=6\text{ seconds} \\ or \\ t+1=0\to t=-1\text{ seconds} \end{gathered}`

Since t = -1 seconds has no sense in this situation, the projectile hits the ground after 6 seconds.