Question

Juan bought a car for $32,560. He knows the car will decrease in value over time. The function rule fx)= 32,560(0.835), where x is the number of years Juan owned the car, can be used to determine thevalue of the car in any given year. The value of the car in different years is shown in the table below.Year the CarWas PurchasedValue of theCar, f(x)Time (years)Since the CarWasPurchased,0123420092010201120122013$32,560$27,188$22.702$18.956$15,828Which of the following is the approximate value of the car in 2020?

Answer 1

Given that Juan bought a car for $32,500, and the function f(x) expressed as

`\begin{gathered} f(x)=32500(0.835)^x \\ \text{where} \\ x\Rightarrow\text{ number of years} \end{gathered}`

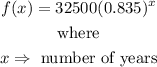
is the value of the car in any given year as shown in the table below:

From the above table, Juan bought the car in 2009.

Thus, to evaluate the approximate value of the car in 2020,

step 1: Evalaute the value of x.

In 2020, the value of x from 2009 will be

`number\text{ of years betw}een\text{ 2009 and 2020 =11}`

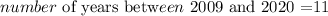
thus,

`x=11`

step 2: substitute 11 for the value of x into the f(x) function.

thus,

`\begin{gathered} f(x)=32500(0.835)^x \\ \text{where x=11} \\ \Rightarrow f(x)=32500(0.835)^(11) \\ =4471.308047 \end{gathered}`

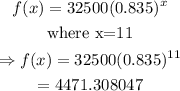
Hence, the approximate value of the car in 2020 is

`\$4480`

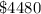
The correct option is B.