Question

A right triangle has legs of lengths 23 inches and 16 inches. Find the length of the hypotenuse. Provide an answer accurate to the nearest tenth.

Answer 1

For any given right angled triangle, the Pythagoras' theorem can be used to solve the misising side given two sides.

For the triangle in this question, we have two sides already given as;

`\begin{gathered} a=23\text{ inches} \\ b=16\text{ inches} \end{gathered}`

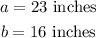
The Pythagoras' theorem is given as;

`c^2=a^2+b^2`

Where c is the hypotenuse (longest side) and a and b are the other two sides.

We can now apply the formula as follows;

`\begin{gathered} c^2=a^2+b^2 \\ c^2=23^2+16^2 \\ c^2=529+256 \\ c^2=785 \\ \end{gathered}`

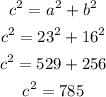
We now take the square root of both sides;

`\begin{gathered} \sqrt[]{c^2}=\sqrt[]{785} \\ c=28.01785 \end{gathered}`

Rounded to the nearest tenth, this now becomes;

`c=28.0`

The digit zero after a decimal is not a significant figure and therefore, we can write it off. Therefore;

`c=28\text{ inches}`

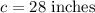
ANSWER:

The hypotenuse is 28 inches