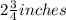Question

Preeta watches an ant and a beetle crawl in a hole in the ground. The beetle is 3/4 inch below ground level.The beetle climbs 1/3 the distance the ant is below ground level. The beetle is now 2 1/2 inches below ground level.(a) Let x = the position of the ant relative to ground level. What equation can be written to solve for x?(b) Solve the equation from Part (a). Show your work.(c) What is the distance between where the ant is and where the beetle is? Answer the question in acomplete sentence. Show your work.

Answer 1

Given:

Initially, the beetle is 3/4 inch below ground level.

The beetle climbs 1/3 the distance the ant is below ground level.

Finally, the beetle is now 2 1/2 inches below ground level.

Step-by-step explanation:

a) To find: The equation

Let x be the position of the ant relative to ground level.

According to the question,

The equation is,

`(1)/(3)x=2(1)/(2)-(3)/(4)`

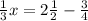
b) To solve for x:

On solving we get,

`\begin{gathered} (1)/(3)x=(5)/(2)-(3)/(4) \\ (1)/(3)x=(7)/(4) \\ x=(21)/(4) \\ x=5(1)/(4) \end{gathered}`

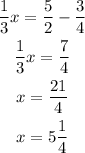
Therefore, the position of the ant relative to ground level is

`5(1)/(4)inches`

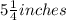
c) To find: The distance between the ant and beetle.

The distance will be,

`\begin{gathered} d=5(1)/(4)-2(1)/(2) \\ =(21)/(4)-(5)/(2) \\ =(11)/(4) \\ d=2(3)/(4)inches \end{gathered}`

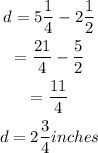
Therefore, the distance between them is,

`2(3)/(4)inches`