Starting from the equation:
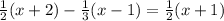
Notice that the coefficients of the binomials are 1/2, -1/3 and 1/2. The least common multiple of 2 and 3 is 6. Multiply both sides of the equation by 6 to get rid of all the denominators:
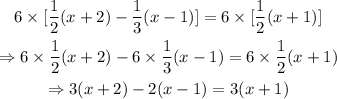
Use the distributive property to expand all the parentheses:
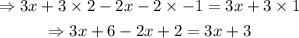
Combine like terms on the left member of the equation:
![undefined]()