Question

Use the Law of Sines to solve (if possible) the triangle for the value of c. Round answers to the nearest tenths. A = 18.92°, a = 48.35 yd, b = 105 yd

Answer 1

First, let's draw a picture of the triangle:

From the law of sines, we have that

`(a)/(sinA)=(b)/(sinB)=(c)/(sinC)`

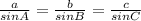
So,we can to find angle B, that is,

`(48.35)/(sin18.92)=(105)/(sinB)`

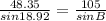
which gives

`sinB=(105sin18.92)/(48.35)`

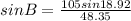
then

`sinB=0.70415`

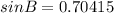
so we have

`B=sin^(-1)0.70415=44.761499`

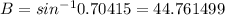
Since interior angles add up to 180, we have that

`\angle C+\angle A+\angle B=180`

which gives

`\angle C+18.92+44.761499=180`

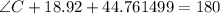
Then, angle C is given as

`\begin{gathered} \angle C=180-116.3185 \\ \angle C=116.3185 \end{gathered}`

Once we have obtained angle C, we can to find side c by substituting the last result into the law of sine from above

`(b)/(sinB)=(c)/(sinC)\Rightarrow(105)/(sin44.761499)=(c)/(sin116.3185)`

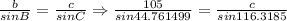
which implies that

`c=(105sin116.3185)/(sin44.761499)`

it yields

`c=(94.1116)/(0.70415)=133.659`

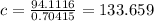
Therefore, by rounding to the nearest tenths, the answer is 133.7 yards