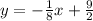To determine the equation of the line, given that you know the slope and the coordinates of one point, you can use the point-slope form, which is:

Where
m is the slope of the line
(x₁,y₁) are the coordinates of the point
Replace the values in the equation
m=-1/8
(x₁,y₁)= (4,4)
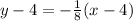
Next, write the equation in slope-intercept form:
-Distribute the multiplication in the parentheses term
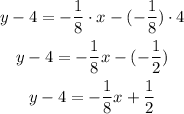
-Add 4 to both sides of the expression
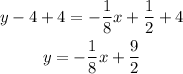
So, the equation of the line with slope -1/8 that passes through the point (4,4) is