Since the tree was broken and the top part forms an angle with the ground, therefore the height of the tree is x+y,
Given the horizontal distance and the angle formed with the ground,
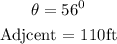
Using SOHCAHTOA, to find x (the vertical part of the broken tree),
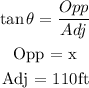
Substituting the values into the formula above,
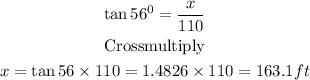
Using the Pythagorean theorem to find y,
![\begin{gathered} y^2=x^2+110^2 \\ y^2=163.1^2+110^2 \\ y^2=26601.61+12100 \\ y^2=38701.61 \\ y=\sqrt[]{38701.61} \\ y=196.7ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v843iojnc9ilbjy48arl22qikppybeqjet.png)
The height of the tree before it got broken is,
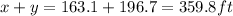
Hence, the height of the tree is 359.8 feet.