Question

Instructions: Find the equation of the line through point (-1,2) and perpendicular to x + 3y = 3. Use a forward slash (i.e. "/") for fractions (e.g. 1/2 for 3).

Answer 1

Let's begin by identifying key information given to us:

The equation passes through the point (-1, 2)

A line is perpendicular to x + 3y = 3

`\begin{gathered} x+3y=3 \\ We\text{ will rearrange the terms to have:} \\ 3y=-x+3 \\ \text{Divide through the terms by the coefficient of y, 3. We have:} \\ (3y)/(3)=-(1)/(3)x+(3)/(3) \\ y=-(1)/(3)x+1 \\ But,y=mx+b \\ \Rightarrow m=-(1)/(3) \\ \therefore m_(perpendicular)=-(1)/(3) \end{gathered}`

For a perpendicular line, the slope is given as the negative reciprocal of the slope of the original line. Mathematically represented thus:

`\begin{gathered} m_(perpendicular)=-(1)/(m) \\ \Rightarrow m=-(1)/(m_(perpendicular)) \\ m=-(1)/(-(1)/(3))=(3)/(1) \\ \Rightarrow m=3 \end{gathered}`

We will proceed to solve for the equation of the original line using the point-slope equation. We have:

`\begin{gathered} y-y_1=m(x-x_1) \\ (x_1,y_1)=(-1,2) \\ m=3 \\ y-2=3(x--1) \\ y-2=3x+3 \\ y=3x+3+2 \\ y=3x+5 \end{gathered}`

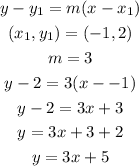
Therefore, the equation of the line that passes through (-1, 2) and is perpendicular to x + 3y = 3 is y = 3x + 5