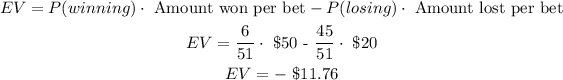Answer
-11.76 dollars
Explanation
First, we need to calculate the probability of winning, that is, the probability of drawing three black cards in succession without replacement.
In the beginning, there are a total of 52 cards, and 26 of them are black, then the probability that the first card drawn is black is:
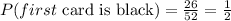
After drawing 1 black card, there are a total of 51 cards, and 25 of them are black, then the probability that the second card drawn is black is:
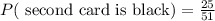
After drawing 2 black cards, there are a total of 50 cards, and 24 of them are black, then the probability that the third card drawn is black is:
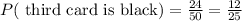
Therefore, the probability of winning, that is, the three cards are black is calculated as follows:
![\begin{gathered} P(\text{ first card is black AND second card is black AND third card is black})=P(\text{ first card is black})\cdot P(\text{ second card is black })\cdot P(\text{ third card is black }) \\ P(winning)=(1)/(2)\cdot(25)/(51)\cdot(12)/(25) \\ P(w\imaginaryI nn\imaginaryI ng)=(6)/(51) \end{gathered}]()
The probability of losing is the complement of the probability of winning, that is,

Finally, the expected value is calculated as follows: