Question

Jane can detail a car by herself in 35 minutes. Sally does the same job in 40 minutes. How long will it take them to detail a car working together? Answer as a fraction?

Answer 1

To solve this question we have to find the rate of each one

∵ Jane can detail a car in 35 minutes

∴ Her rate = 1/35

∵ Sally can do the same job in 40 minutes

∴ Her rate = 1/40

∵ They are working together to do the same rate

Assume that they will work for t minutes, then

`\therefore(1)/(35)* t+(1)/(40)* t=1`

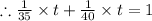
Now we will add the 2 fractions

`\begin{gathered} \because(1)/(35)t+(1)/(40)t=1 \\ \therefore(1(40)t+1(35)t)/((35)(40))=1 \\ \therefore(40t+35t)/(1400)=1 \\ \therefore(75t)/(1400)=1 \end{gathered}`

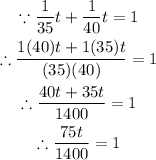
By using cross multiplication

`\therefore75t=1400`

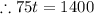
Divide both sides by 75

`\begin{gathered} \because(75t)/(75)=(1400)/(75) \\ \therefore t=(56)/(3) \end{gathered}`

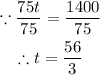
They will take 56/3 minutes t finish the job together

You can write it as a mixed number 18 2/3 minutes