First, draw a diagram to visualize the situation:
According to Newton's Law of Universal Gravitation, each mass exerts an attractive force on each of the other masses (let's analyze what happens with the 69.8kg mass), whose magnitude is given by:
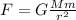
Where G is the gravitational constant:
![G=6.672*10^(-11)N\frac{m^2}{\operatorname{kg}^2}]()
And the variables M, m and r correspond to the masses of the two objects involved in the interaction and the distance between them.
Find the magnitude of each of the gravitational forces acting on the object with mass 69.8kg. Then, substract them to find the net force, since they point in opposite directions.
The force exerted by the 212 kg mass is:
![\begin{gathered} F_(212)=(6.672*10^(-11)N\frac{m^2}{\operatorname{kg}^2})*\frac{212\operatorname{kg}*69.8\operatorname{kg}}{(0.1875m)^2} \\ =2.81*10^(-5)N \end{gathered}]()
The force exerted by the 222kg mass is:
![\begin{gathered} F_(222)=(6.672*10^(-11)N\frac{m^2}{\operatorname{kg}^2})*\frac{222\operatorname{kg}*69.8\operatorname{kg}}{(0.1875m)^2} \\ =2.94*10^(-5)N \end{gathered}]()
Then, the net force acting on the mass of 69.8kg is:
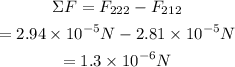
Therefore, the value of the net gravitational force exerted by the two larger masses on the 69.8kg mas, is: 1.3*10^-6 N.