14300 meters
Step-by-step explanation
we need assume a rigth triangle and then,
Step 1
Let
opposite side=height= 1000 mt
adjacent side=distance from the base tof the cliff ot the place where the glider lands=x
angle= 4
now, we need a function that relates those measures
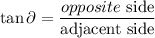
replace,
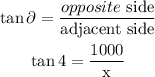
Step 2
now, solve for x
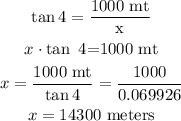
I hope this helps you