Solution
For this case we can do the following
V_L= L*w*h = 8*w*delta x
then we can create the following relation:
3/3 = (3-x)/w
w = 3-x
Then replacing in the slice volume we have:
V_L = 8*(3-x)*delta x
The force is given by:
F= rho * V_L = 10 N/m^3 * 8* (3-x)* delta x
Displacement = 2+x
then the total work is given by:
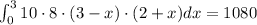
If we solve the integral we got:
1080 J