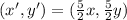Question

8.1Figure LMNOPQ is dilated usingthe origin as the center of dilation tocreate L'M'N'O'P'Q'. Both figures areshown on the grid.ܝ ܟ ܗ ܢ ܘ ܠ ܐ ܗ ܘL67 8 9 10-10-9-8-7 -6 -5 4m-22-3Q0Pi.roo-10What algebraic rule best representsthe effect of the dilation on thecoordinates of LMNOPQ?

Answer 1

Identify the coordinates of Q and Q'.

`Q(-4,-2);Q^(\prime)(-10,-5)`

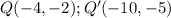
Compare the two sets of coordinates. Divide the coordinate of the new figure by the coordinate of the original figure. Thus, we have the following.

`\begin{gathered} x-coordinates\colon(x^(\prime))/(x)=(-10)/(-4)=(5)/(2) \\ y-coordinates\colon(y^(\prime))/(y)=(-5)/(-2)=(5)/(2) \end{gathered}`

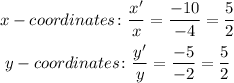
This means the coordinates of the bigger polygon can be obtained by getting the 5/2 of the original coordinates. Thus, the new coordinates must be

`(x^(\prime),y^(\prime))=\mleft((5)/(2)x,(5)/(2)y\mright)`