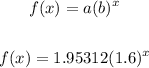Given:
The point of the graph
(2,5), (3,8)
Find-:
The equation of the graph
Explanation-:
Let the equation is:
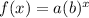
Give points are,
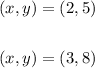
If the point on the graph then the equation specified the graph then,
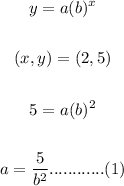
For the second point
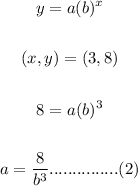
From eq(1) and eq(2), value of "a" is equal then,
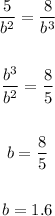
So the value of "a" is:
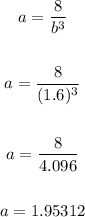
So the equation becomes,