Question

What is the average rate of change of the function f(x)=4x^2+3x on the interval [1,5]

Answer 1

7, though I don't know if it's 100% correct. I tried to help.

Explanation:

f(x) = 4x^2 + 3x interval [1,5]

f(1) = 4(1)^2 + 3(1)

f(1) = 4 + 3

f(1) = 7

Answer 2

`\boxed {\boxed {\sf 27}}`

Explanation:

The average rate of change is the change in the output from one input to another. Essentially, it is the change in y over the change in x.

`\frac {\Delta y}{\Delta x} = \frac { f (x_2)- f(x_1) }{x_2-x_1}`

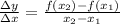
Let's assign 1 to x₁ and 5 to x₂.

`\frac {f(5)-f(1)}{5-1}`

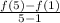
We must find the outputs f(5) and f(1). Substitute the value in for each x in the function.

f(x)= 4x² + 3x

• f(5) = 4(5)² + 3(5)

• f(5)= 4(25) + 15

• f(5) = 100 + 15 =115

• f(1)= 4(1)² + 3(1)

• f(1)= 4(1) + 3

• f(1)= 4+ 3 =7

Now we can find the average rate of change. We know the outputs and we know the inputs.

`\frac {f(5)-f(1)}{5-1}`

`\frac {115 -7}{5-1}`

`\frac {108}{4}`

`27`

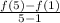
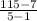
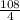
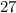
The average of change of the function f(x) = 4x² + 3x on the interval [1,5] is 27.