Question

Oscar buys his lunch in the school cafeteria. the cost of 15 school lunches is $33.75.Which graph has a slope that beat represents the average cost of the lunches in dollars per lunch?

Answer 1

Graph A best has the slope that represents the average cost of the lunches in dollars per lunch

Here, we want to select the graph that has an average cost of the lunches in dollars per lunch

From what we have, the average cost of the lunches will be the cost of the lunches divided by the number of lunches

Mathematically, we have that as;

`(33.75)/(15)\text{ = \$2.25 per lunch}`

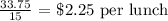
Now, we want to select which of the plots has this as its slope

Looking at the graphs, we select any two points and apply the slope formula

For the first graph, we have;

(8,18) and (1,2)

We have the slope calculation as follows;

`m\text{ = }\frac{y_2-y_1}{x_2-x_1\text{ }}\text{ = }(2-18)/(1-8)\text{ = 2.29}`

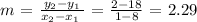
This is not correct

We move on the second graph

We have the points at (4,2) and (8,4)

We have the slope as;

`(4-2)/(8-4)\text{ = }(1)/(2)\text{ = 0.5}`

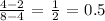
This is also incorrect

For the third graph, we have the points (1,6) and (2,13)

We have this as;

`(13-6)/(2-1)\text{ = 7 }`

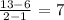
Now as we can see, we can only have an approximate answer and thus, the closest answer so far is the first option as it is approximately equal to the calculated value

Hence, the first graph will give the correct representation

Kindly note that w