Question

Suppose that grade point averages of undergraduate students at one university have a bell-shaped distribution with a mean of 2.54 and a standard deviation of 0.41Using the empirical rule, what percentage of the students have grade point averages that are less than 2.957 Please do not round your answerAnswerHow to enter your answer (Opens in new window)1 TablesKeypadKeyboard Shortcuts%Submit Answer80°F AE

Answer 1

Step-by-step explanation:

We were given the following information:

This is a normal (bell-shaped) distribution having:

Mean = 2.54

Standard deviation = 0.41

x = 2.957

The empirical rule is a rule in statistics that states that almost all observed data will fall within three standard deviations of the mean, for a normal distribution.

We calculate the z-score as shown below:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ z=(2.957-2.54)/(0.41) \\ z=(0.417)/(0.41) \\ z=1.017\approx1 \\ z=1 \end{gathered}`

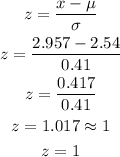
This means that 2.957 is about 1 standard deviation above the mean

Much more directly, the empirical rule predicts that 68% of observations falls within the first standard deviation, 95% within the first two standard deviations, and 99.7% within the first three standard deviations

To obtain the percentage of students having a GPA less than 2.957, we have:

`\begin{gathered} =68+(1)/(2) \\ =68+0.5 \\ =68.5\text{ \%} \end{gathered}`

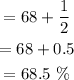
Hence, 68.5% of the students have grade point averages less than 2.957