Answer:
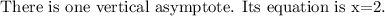
Explanation:
Oblique asymptotes occur when the degree of the denominator of a rational function is one less than the degree of the numerator.
If the degree of the denominator is equal to the degree of the numerator, there will be a horizontal asymptote at the ratio between the coefficients of the highest degree of the function. A horizontal asymptote at y = 0 means that the degree of the denominator is greater than the degree of the numerator
A vertical asymptote with a rational function occurs when there is division by zero.
Therefore, for the given function:
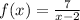
Since for x=2 the denominator could be 0, there is a vertical asymptote at x=2.
Horizontal asymptote at y=0 means that the degree of the denominator is greater than the degree of the numerator.