Answer:
P = $300
r = 0.15
n = 12
$544.61 (to the nearest cent)
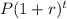
$524.70 (to the nearest cent)
Explanation:
P = principal amount = $300
r = annual interest rate in decimal form = 15% = 15/100 = 0.15
n = number of times interest is compounded per unit t = 12
How much she'll owe in 4 years
P = 300
r = 0.15
n = 12
t = 4
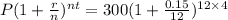
= $544.61 (to the nearest cent)
Yearly compounding interest rate
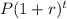
How much she'll owe in 4 years at yearly compounding interest
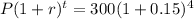
= $524.70 (to the nearest cent)