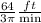Question

Grain pouring from a chute at the rate of 12 ft^3/min forms a conical pile whose height is always 4 times its radius. How fast is the height of the pile increasing at the instant the pile is 3 ft. high?

Answer 1

Given:

The rate of grain pouring from chute is given as

`(dV)/(dt)=12\text{ }(ft^3)/(\min )`

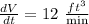
The relation between height and radius is given

`h=4r`

It is also given that height is h=3 ft.

Step-by-step explanation:

The volume of cone is

`V=(1)/(3)\pi(r^2)h`

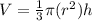
Substitute the value of h=4r.

`V=(1)/(3)\pi((h)/(4))^2h=(\pi)/(48)h^3`

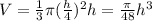
Now take the derivative of the volume with respect to t,

`\frac{dV}{d\text{ t}}=(\pi)/(48)*3h^2*\frac{dh}{\text{ dt}}`

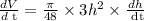
Substitute the value of h and dh/dt,

`12=(\pi)/(48)*3*9*(dh)/(dt)`
`(12*48)/(\pi*3*9)=\frac{dh}{d\text{ t}}`
`(dh)/(dt)=(4*16)/(\pi*3)=(64)/(3\pi)(ft)/(\min )`

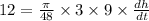
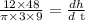
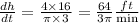
Answer:

Hence the height increasing at the rate of

`(64)/(3\pi)(ft)/(\min )`