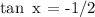Question

Find the value of tan x if tan 2x=4/3

Answer 1

`\tan \text{ x = -}(1)/(2)`

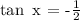
Step-by-step explanation:

Here, we want to get the value of tan x

We start with the following trigonometric identities formula

We have this as:

`\tan \text{ 2x }=\text{ }\frac{2\text{ tan x}}{1-\tan ^2x}`

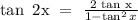
Let tan x = b

`(4)/(3)\text{ = }(2b)/(1-b^2)`

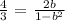
Now, let us solve for b

`\begin{gathered} 3(2b)=4(1-b^2) \\ 6b=4-4b^2 \\ 4b^2+6b-4\text{ = 0} \\ 2b^2-3b-2\text{ = 0} \end{gathered}`

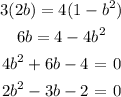
We proceed to solve the quadratic equation as follows:

`\begin{gathered} 2b^2-4b+b-2\text{ = 0} \\ 2b(b-2)\text{ + 1(b-2) = 0} \\ (2b+1)(b-2)=0_{} \\ 2b\text{ + 1 = 0 or b-2 = 0} \\ b\text{ = -1/2 or b = 2} \\ \end{gathered}`

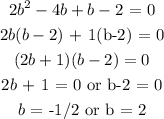
Thus, we have it that:

`\begin{gathered} \tan \text{ x = 2} \\ or\text{ } \\ \tan \text{ x = -1/2} \end{gathered}`

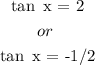
However, tan x = 2 will not be correct

This is because it will give a negative value of tan 2x

The only answer accepted is thus:

`\tan \text{ x = -1/2}`
`\begin{gathered} \text{if tan x = 2} \\ \tan \text{ 2x = }(2(2))/(1-(2)^2)\text{ = }(4)/(-3)\text{ = -}(4)/(3) \\ \\ \text{if tan x = -1/2} \\ \tan \text{ 2x =}(2(-(1)/(2)))/(1-(-(1)/(2))^2)\text{ = }(-1)/(1-(1)/(4))\text{ =}(-1)/(-(3)/(4))\text{ = }(4)/(3) \end{gathered}`