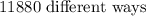Question

There are 12 students in a homeroom. How may different ways can they be chosen tobe elected President, Vice President, Treasurer, and Secretary?

Answer 1

Given that:

- There are a total of 12 students in a homeroom.

- There must be a President, a Vice President, a Treasurer, and a Secretary.

You need to remember the Permutation Formula:

`_nP_r=(n!)/((n-r)!)`

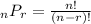
Where "n" is the total number of objects and "r" is the number of objects chosen from the total number.

In this case, you can identify that:

`\begin{gathered} n=12 \\ r=4 \end{gathered}`

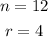
Therefore, substituting values into the formula and evaluating, you get:

`\begin{gathered} _(12)P_4=(12!)/((12-4)!) \\ \\ _(12)P_4=(12!)/((8)!) \end{gathered}`
`_(12)P_4=(12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)/(8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)`
`\begin{gathered} _(12)P_4=(479001600)/(40320) \\ \end{gathered}`
`_(12)P_4=11880`

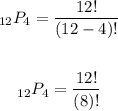
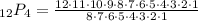
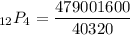
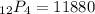
Hence, the answer is:

`11880\text{ different ways}`