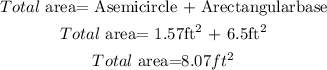Question

An architect is designing a Norman window which is comprised of a rectangular base and semicircle top as shown in the figure to the right.a) Calculate the perimeter of the window to determine how much trim is needed.b) Calculate the area of the window to determine the square feet of glass needed.

Answer 1

To find out the permiter of the window we have to find out the perimeter of each figure. The perimeter is the sum of all sides.

First, let's find out the rectangular base minus the inner side that it's with the semicircle (2ft)

`\begin{gathered} P=\text{ 2ft + 3.25 ft + 3.25 ft} \\ P=\text{ 2ft + 6.5ft} \\ Prectangular\text{ base}=\text{ 8.5ft} \\ \end{gathered}`

Now, we find out the perimeter if the semicircle top:

`\begin{gathered} If\text{ the perimeter of a circle is 2}\pi r,\text{ and the diameter is of the circle is: 2ft} \\ Then,\text{ the radius of the circle is: }(2)/(2)=\text{ 1 ft} \\ So,\text{ the perimeter of the semicircle will be =}(2\pi r)/(2) \\ Psemicircle=(2\pi r)/(2) \\ Psemicircle=\text{ }\pi(1) \\ Psemicircle=\text{ 3.1415ft} \\ \\ \end{gathered}`

So, the total perimeter of the window will be the sum of both perimeters:

`\begin{gathered} Total\text{ perimeter =}Psemicircle\text{ + Prectangularbase} \\ Total\text{ Perimeter= 3.1415ft + 8.5ft} \\ Total\text{ perimeter=}11.64ft \end{gathered}`

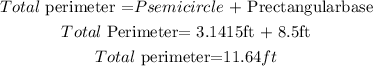
B) To calculate the area of the window, we have to also find out the area of each figure. So let's find out first the rectangular base:

`\begin{gathered} Arectangular\text{ base=base x height } \\ Arectangularbase=\text{ 2 x 3.25ft} \\ Arectangularbase=6.5ft^2 \end{gathered}`

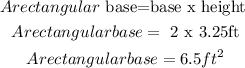
Then, let's find out the area of the semicircle:

`\begin{gathered} Area\text{ of a circle= }\pi r^2 \\ \\ Area\text{ of a semicircle= }(\pi r^2)/(2) \\ \\ Areasemicirlce=\text{ }(\pi(1)^2)/(2) \\ \\ Asemicircle=\text{ }(\pi)/(2) \\ \\ Asemicircle=\text{ 1.57ft}^2 \end{gathered}`

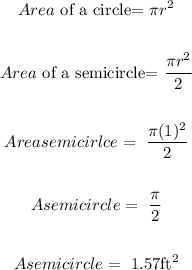
Now, to find out the total area of the window we have to add both areas of the figures. Then:

`\begin{gathered} Total\text{ area= Asemicircle + Arectangularbase} \\ Total\text{ area= 1.57ft}^2\text{ + 6.5ft}^2 \\ Total\text{ area=}8.07ft^2 \end{gathered}`