Answer: The expected value of the game to the player is $ 0.53( It means losing), and the amount expected to lose when the game is played 1000 times is $ 530.
Step-by-step explanation:
Given:
The winning amount of the player = $350
The probability of winning the game = 1/38
The amount that the player gets to keep to play the game=$10
Since the probability of winning the game is 1/38, the probability of losing the game is 1-1/38.
To find the expected value of the game to the player, we use:
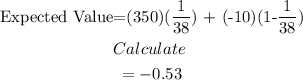
Expected value= - $ 0.53( It means losing)
The amount expected to lose when the game is played 1000 times is:
1000($ 0.53) =$ 530
Therefore, the expected value of the game to the player is $ 0.53( It means losing), and the amount expected to lose when the game is played 1000 times is $ 530.