Here we can solve this question by the below equation,
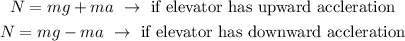
Here N = mass of the student When he is in the accelerated elevator.
mg is the mass of the student before entering the elevator
And (a) is the acceleration of the elevator
Now,
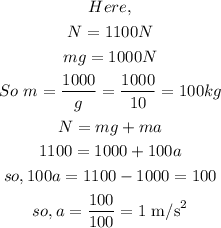
Now when elevator is accelerating upward the acceleration feel by the pendulum and the student will be = 10 + 1 = 11 m/s^2
And we know that time period of pendulum is,
![\begin{gathered} T=2\pi\sqrt[\placeholder{⬚}]{(l)/(g)} \\ When\text{ elevator was at rest then,} \\ l=((T)/(2\pi))^2g=((3)/(2*3.14))^210=0.228*10=2.28 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/2dcjr6qa625c1wh7m0g8tmx242094lvl06.png)
now when elevator is accelerated,
![T=2\pi\sqrt[\placeholder{⬚}]{(l)/(g)}=2*3.14*\sqrt[\placeholder{⬚}]{(2.28)/(11)}=\text{ 2.85}](https://img.qammunity.org/2023/formulas/physics/college/tho5g6jh12k6cy2fq326cgjs8oyfjakwom.png)
so o