The right triangle has a hypotenuse of 80in and its shortest leg is 48in.
You can make a sketch of the triangle to visualize the figure:
To determine the measure of the missing leg you can apply the Pythagorean theorem. This theorem states that the square of the hypothenuse (c) of a right triangle is equal to the sum of the squares of its legs (a and b) so that:
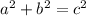
The missing side is the longers leg "b", to determine its length you have to write the expression above for b.
To do so, first, pass a² to the right side of the expression by applying the opposite operation to both sides of it, which means you have to subtract it:
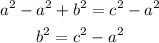
Second, since we need to find the value of b, is to calculate the square root of b², so that the exponent is canceled, and, for the equality to be valid, any operation that is done to one side of the equation must be done to the other side, so you have to apply the square root to both sides of the equal sign:
![\begin{gathered} \sqrt[]{b^2}=\sqrt[]{c^2-a^2} \\ b=\sqrt[]{c^2-a^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/3g43jh6zpj7jvy3mia3o2rspbwe14hwefr.png)
Now that we have the formula to calculate b, what is left is to replace it with the known measures of the triangle c=80 and a=48
![\begin{gathered} b=\sqrt[]{80^2-48^2} \\ b=\sqrt[]{6400-2304} \\ b=\sqrt[]{4096} \\ b=64 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wdrklq6nsexovrpjg0krvftfwrhw0isvow.png)
The measure of the other leg of the right triangle is 64in.