Question

mlal-Question 24 of 502 PoinSolve the equation f(z) = 2r² - 92³ +172²-16z +6 given that one of its roots is z=1+OA== (3/2,1,1+i, -1- i}OB. == (3/2,1}Ocz= (3/2,1,1+1,1-i}ODz={1+1, 1-i}Reset Selection

Answer 1

Given:

`f(x)=2x^4-9x^3+17x^2-16x+6`

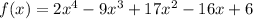
We have one root: 1+ i

Let's find the remaining roots.

Given that the root is a complex root, complex roots come in conjugate pairs.

Thus, we have:

1+i and 1 - i

In the factored form we have

(x - 1+i) = 0

(x - 1 - i) = 0

Thus, we have:

Thus, we have:

`\begin{gathered} (x-1+i)(x-1-i)=0 \\ \\ \text{ Expand:} \\ x^2-2x+2 \end{gathered}`

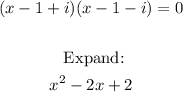
Now, divide using the long division method:

`(2x^4-9x^3+17x^2-16x+6)/(x^2-2x+2)=2x^2-5x+3`

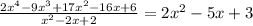
The quotient after using the long division method to divide is:

`2x^2-5x+3`

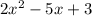
Factor the quotient by grouping:

`\begin{gathered} 2x^2-5x+3=0 \\ \\ 2x^2-2x-3x+3=0 \\ \\ (2x^2-2x)-2x+3=0 \\ \\ Factor\text{ 2x from the first group:} \\ 2x(x-1)-3x+3=0 \\ \\ Factor\text{ 3 from the second group:} \\ 2x(x-1)-3(x-1)=0 \\ \\ (2x-3)(x-1)=0 \end{gathered}`

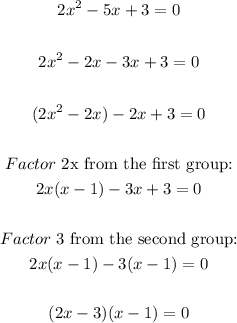
Solve each factor for x:

`\begin{gathered} 2x-3=0 \\ 2x=3 \\ x=(3)/(2) \\ \\ \\ x-1=0 \\ x=1 \end{gathered}`

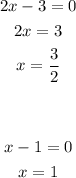
Therefore, the roots of the function are:

`x=(3)/(2),1,1+i,1-i`

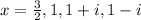
ANSWER: C

The remaining roots are:

3/2, 1