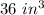Question

Rectangular prism J is 2 in tall, 4 in wide, and 3 inches deep. The volume of Jis twice the volume of right rectangular prism K What is the total volume of these two figures? I

Answer 1

The total volume of the two figures is;

`36\text{ }in^3`

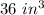
Step-by-step explanation:

Given that the Rectangular prism J has the dimensions;

2 in tall, 4 in wide, and 3 inches deep;

`\begin{gathered} l=2\text{ in} \\ b=4\text{ in} \\ h=3\text{ in} \end{gathered}`

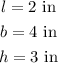
Recall that the volume of a prism can be calculated using the formula;

`V=l* b* h`

substituting the given values;

`\begin{gathered} V_J=2*4*3in^3 \\ V_J=24\text{ }in^3 \end{gathered}`

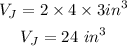
Also given that the volume of J is twice the volume of right rectangular prism K.

`\begin{gathered} V_J=2V_K \\ V_K=(V_J)/(2)=(24)/(2) \\ V_K=12\text{ }in^3 \end{gathered}`

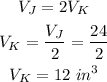
The total volume of these two figures will then be;

`\begin{gathered} V_T=V_J+V_K \\ V_T=(24+12)in^3 \\ V_T=36\text{ }in^3 \end{gathered}`

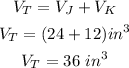
Therefore, the total volume of the two figures is;

`36\text{ }in^3`