Question

The population of a small town in central Florida has shown a linear decline in the years 1995-2005. In 1995 the population was 24100 people. In 2005 it was 14800 people.

Answer 1

Part A:

Since the population is showing a linear decline, we can express the function P(t) as

`\begin{gathered} y=mx+b \\ \text{where} \\ m\text{ is the slope} \\ b\text{ is the y-intercept} \end{gathered}`

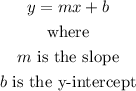
Given two points

(1995,24100), and (2005,14800)

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \text{IF }\mleft(x_1,y_1\mright)=\mleft(1995,24100\mright),\text{ and }(x_2,y_2)=\mleft(2005,14800\mright),\text{ THEN} \\ \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(14800-24100)/(2005-1995) \\ m=(-9300)/(10) \\ m=-930 \end{gathered}`

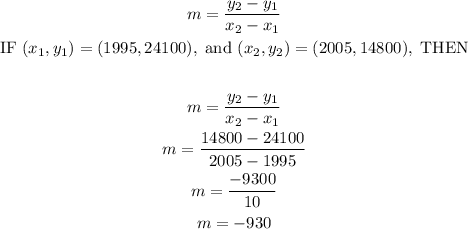
Now that we have solved for the slope, we can now solve for the y-intercept. We will use the point (2005,14800), but using (1995,24100) will work just as well.

`\begin{gathered} \text{IF }m=-930,\text{ and }(x,y)=\mleft(2005,14800\mright),\text{ THEN} \\ \\ y=mx+b \\ 14800=(-930)(2005)+b \\ 14800=-1864650+b \\ 14800+1864650=+b \\ 1879450=b \\ b=1879450 \end{gathered}`

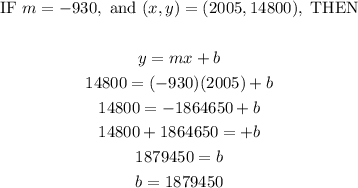
Convert the function x into a function of time t, then the the function is

`P(t)=-930t+1879450`

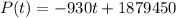
Part 2:

What will be the population in 2007.

Substitute t = 2007.

`\begin{gathered} P(t)=-930t+1879450 \\ P(2007)=-930(2007)+1879450 \\ P(2007)=-1866510+1879450 \\ P(2007)=12940 \end{gathered}`

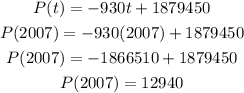
Therefore, in the year 2007, the population will be 12940.