Question

**PRE CALCULUS SUBJECT**Can someone help me with this practice problem? I need it answered

Answer 1

m X H = [-9 36 -9/2]

Step-by-step explanation:

First, let's find m:

Since the first two matrices are equal:

`\begin{gathered} (2)/(3)m=3 \\ 2m=3\cdot3 \\ m=(9)/(2) \end{gathered}`

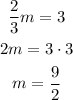
Now, let's find H:

Let's say H = [H₁ H₂ H₃]

So,

([H₁ H₂ H₃] + [1 4 -2]) + [3 2 -6] = [-2 8 -1] + ([1 4 +2] + [3 2 -6])

We can sum the matrixes of each side of the equality and compare with the other side:

[H₁ H₂ H₃] + [1 4 -2] + [3 2 -6] = [-2 8 -1] + [1 4 -2] + [3 2 -6]

H₁ + 1 + 3 = -2 + 1 + 3

H₁ + 4 = 2

H₁ = -2

H₂ + 4 + 2 = 8 + 4 + 2

H₂ + 6 = 14

H₂ = 14 - 6

H₂ = 8

H₃ - 2 - 6 = -1 - 2 - 6

H₃ - 8 = -9

H₃ = -9 + 8

H₃ = -1

So,

H = [-2 8 -1]

And,

m X H = 9/2 [-2 8 -1]

m X H = [9/2*(-2) 9/2*(8) 9/2*(-1)]

m X H = [-9 36 -9/2]