Answer:
x² = 4y/3
Step-by-step explanation:
The standard form of the parabola is
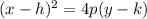
Where (h, k) is the vertex and p is a number determined by the focus because the focus is located (h, k+p).
In this case, (h, k) = (0, 0), so the focus is also equal to
focus = (0, 1/3) = (0, 0 + p)
It means that
1/3 = 0 + p
1/3 = p
Then, replacing (h, k) = (0, 0) and p = 1/3, we get that the equation of the parabola is
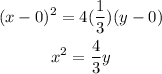
Therefore, the answer is
x² = 4y/3