Answer:
13 1/3 hours.
Step-by-step explanation:
First, we determine the rates of filling and draining the pool.

Let x be the time taken to fill the pool by the inlet pipe if the drain is left open:
Therefore:
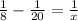
Next, solve for x:
Take the lowest common multiple of the left-hand side:
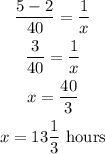
It will take 13 1/3 hours to fill the pool.