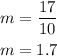To find the Constant rate of change of "y" with respect to "x", you can apply the formula for calculate the slope of a line. This is:

You know that this line passes through the points (-1.6, 2.6) and (2.5, 9.57). Then, you can set up the following:
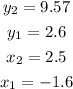
Now you must substitute the corresponding coordinates into the formula for calculate the slope of a line:

Evaluating, you get that the constant rate of change of "y" with respect to "x" is: