THe probability is 0.047.
Given:
Number of red marbles is, n(R) = 9.
Number of blue marbles is, n(B) = 3.
Number of green marbles is, n(G) = 4.
The objective is to daw a blue marble and then a green marble with replacement.
The total number of marbles is,
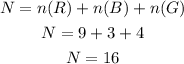
Now, the probability of drawing a blue marble and then a green marble with replacement will be,
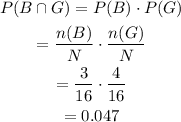
Hence, the required probability is 0.047.