Question

A Fibonacci-like sequence has the first two terms of -9 and -3. Find the first 20 terms.

Answer 1

In the Fibonacci sequence of:

T1,T2,T3,......

T3=T2+T1

T4=T3+T2

T5=T4+T3

And the sequence continues like that, the next term is a summation of the previous two.

So with this knowledge, we can find the first 20 terms of the sequence in

question.

`\begin{gathered} F_1=-9 \\ F_2=-3 \\ F_3=F_2+F_1=-3+(-9)=-12 \\ F_3=-12 \end{gathered}`
`\begin{gathered} F_4=-12+(-3) \\ =-12-3 \\ F_4=-15 \\ \end{gathered}`
`\begin{gathered} F_5=-15+(-12) \\ =-15-12 \\ F_5=-27 \end{gathered}`
`\begin{gathered} F_6=-27+(-15) \\ -27-15 \\ F_6=-42 \end{gathered}`
`\begin{gathered} F_7=-42+(-27) \\ =-42-27 \\ F_7=-69 \end{gathered}`
`\begin{gathered} F_8=-69+(-42) \\ =-69-42 \\ F_8=-111 \end{gathered}`
`\begin{gathered} F_9=-111+(-69)_{}_{} \\ =-111-69 \\ F_9=-180 \end{gathered}`
`\begin{gathered} F_(10)=-180+(-111) \\ =-180-111 \\ F_(10)=-291 \end{gathered}`

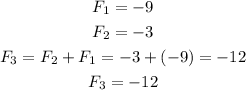
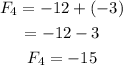
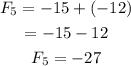
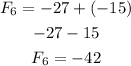
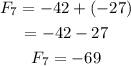
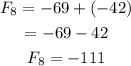
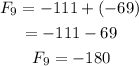
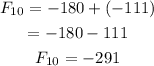
Therefore, the first 10 terms are -9,-3,-12,-15,-27,-42,-69,-111,-180,-291.