Question

A string on a violin is 25.4 cm long produces a fundamental frequency of 440 Hz. What must its length be shortened to in order to produce a tone with a frequency of 523.3 Hz?

Answer 1

Given,

The length of the string, L₁=25.4 cm

The fundamental frequency, f₁=440 Hz

The new frequency, f₂=523.3 Hz

The frequency of a standing wave is related to the length of the string as,

`f=(v)/(2L)`

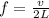
On rearranging the above equation,

`\begin{gathered} fL=(v)/(2) \\ \Rightarrow fL=\text{ constant} \\ \Rightarrow f_1L_1=f_2L_2 \end{gathered}`

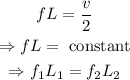
Where L₂ is the shortened length of the string.

On substituting the known values,

`\begin{gathered} 440*25.4=523.3* L_2 \\ L_2=(440*25.4)/(523.3) \\ =21.36\text{ cm} \end{gathered}`

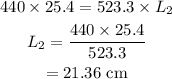
Therefore the shortened length of the string in order to produce the required frequency is 21.36 cm.