When we divide to polynomials, let's say p(x) and q(x), the result of this division can be written as:
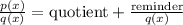
In this case we have q(x)=x-1, the quotient is 1 and the reminder -3 then we have:
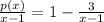
So we have an equation for p(x). We can multiply both sides by x-1:
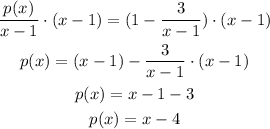
Then p(x)=x-4.
We still need to find the horizontal asymptote and y-intercept of p(x)/(x-1). This expression is:
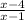
Since both the numerator and the denominator have the same degree (i.e. the biggest power of x in both expressions is the same) then the horizontal asymptote is given by:
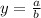
Where a and b are the leading coefficients of the numerator and the denominator respectively. The leading coefficient of a polynomial is the number multiplying the biggest power of x and in both cases this number is 1. Then a=1 and b=1 and the horizontal asymptote is y=1.
Finally the y intercept is the point (0,y) so we just need to take x=0 and solve:
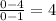
Then the y-intercept is (0,4).