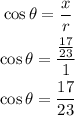Question

The terminal side of angle θ intersects the unit circle in the first quadrant at x= 17/23. What are the exact values of sin θ and cos θ?

Answer 1

`\begin{gathered} \sin \theta=\frac{4\sqrt[]{15}}{23} \\ \cos \theta=(17)/(23) \end{gathered}`

Step-by-step explanation:

In a unit circle, the radius = 1 unit

The terminal side of angle θ intersects the unit circle in the first quadrant at x= 17/23.

From the equation of a unit circle, we have:

`x^2+y^2=1^2`

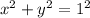
Substitute the given value of x:

`\begin{gathered} ((17)/(23))^2+y^2=1^2 \\ y^2=1-((17)/(23))^2 \\ y^2=(240)/(529) \\ y=\pm\sqrt[]{(240)/(529)} \\ y=\pm\frac{4\sqrt[]{15}}{23} \end{gathered}`

Since angle θ is in the first quadrant, we take the positive value of y:

Therefore:

`\begin{gathered} \sin \theta=(y)/(r) \\ \sin \theta=\frac{\frac{4\sqrt[]{15}}{23}}{1} \\ \sin \theta=\frac{4\sqrt[]{15}}{23} \end{gathered}`

Similarly:

`\begin{gathered} \cos \theta=(x)/(r) \\ \cos \theta=((17)/(23))/(1) \\ \cos \theta=(17)/(23) \end{gathered}`