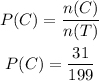Question

4. In a survey, 31 people indicated that they prefer cats, 55 indicated that they prefer dogs, and 113 indicated that they don't enjoy either pet. Find the probability that a randomly chosen person will prefer cats.

Answer 1

In a survey;

Number of people that indicated they prefer cats = 31

Number of people that indicated they prefer dogs = 55

Number of people that indicated they don't enjoy either pets = 113

Total number of people involved in the survey is;

`31+55+113=199`

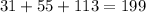
The probability of an event is the number of favorable outcomes divided by the total number of outcomes possible. Thus, we have;

`\begin{gathered} P(E)=(n(E))/(n(T)) \\ \text{Where P(E)= probability of an even} \\ n(E)=\text{ number of the event} \\ n(T)=total\text{ outcomes of events} \end{gathered}`

Hence, the probability that a randomly chosen person will prefer cats is;

`\begin{gathered} P(C)=(n\mleft(C\mright))/(n(T)) \\ P(C)=(31)/(199) \end{gathered}`