SOLUTION
Write out the given expression
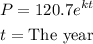
In 2009, the population is 167,025 implies
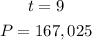
To obtain the value of K, substitute the given value into the expression

Divide both sides by 120.7
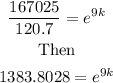
Then take natural logarithm of both sides
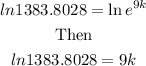
Then, Divide both sides by 9

Therefore
The value of k is 0.8036
B).Using the given model, the population in 2020 will be

The population will be
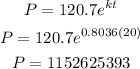
Therefore, the population in 2020 is 1152625393 thousand people
The Population for 2025 will be
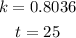
Then
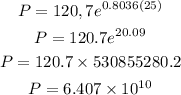
Therefore, the population for 2025 is 6.407x10^10
C).P=220,000

Then substitute the values into the expression

Take the natural logarithm of the equation in the last line
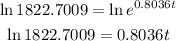
Then divide both sides by t

Hence
The population will reach 220000 in 9years