Question

The population P (in thousands) of a certain city from 2000 through 2014 can be modeled by P = 120.7ekt, where t represents the year, with t = 0 corresponding to 2000. In 2009, the population of the city was about 167,025.(a) Find the value of k. (Round your answer to four decimal places.)k=2)(b) Use the model to predict the populations of the city (in thousands) in 2020 and 2025. (Round your answers to three decimal places.)2020 P = thousand people2025 P = thousand people(c) According to the model, during what year will the population reach 220,000?anser=

Answer 1

Write out the given expression

`\begin{gathered} P=120.7e^(kt) \\ t=\text{The year} \end{gathered}`

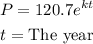
In 2009, the population is 167,025 implies

`\begin{gathered} t=9 \\ P=167,025 \end{gathered}`

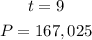
To obtain the value of K, substitute the given value into the expression

`\begin{gathered} 167,025=120.7e^(k(9)) \\ 167,025=120.7e^(9k) \end{gathered}`

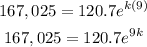
Divide both sides by 120.7

`\begin{gathered} (167025)/(120.7)=e^(9k) \\ \text{Then} \\ 1383.8028=e^(9k) \\ \end{gathered}`

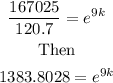
Then take natural logarithm of both sides

`\begin{gathered} ln1383.8028=\ln e^(9k) \\ \text{Then} \\ ln1383.8028=9k \\ \end{gathered}`

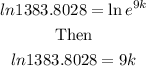
Then, Divide both sides by 9

`\begin{gathered} k=(ln1383.8028)/(9) \\ \text{Then} \\ k=0.8036 \end{gathered}`

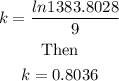
Therefore

The value of k is 0.8036

B).Using the given model, the population in 2020 will be

`\begin{gathered} \text{For the 2020, } \\ t=20 \\ k=0.8036 \end{gathered}`

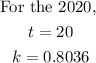
The population will be

`\begin{gathered} P=120.7e^(kt) \\ P=120.7e^(0.8036(20)) \\ P=1152625393 \end{gathered}`

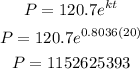
Therefore, the population in 2020 is 1152625393 thousand people

The Population for 2025 will be

`\begin{gathered} k=0.8036 \\ t=25 \end{gathered}`

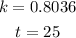
Then

`\begin{gathered} P=120,7e^(0.8036(25)) \\ P=120.7e^(20.09) \\ P=120.7*530855280.2 \\ P=6.407*10^(10) \end{gathered}`

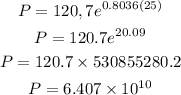
Therefore, the population for 2025 is 6.407x10^10

C).P=220,000

`\begin{gathered} P=120.7e^{^(kt)} \\ \text{Where } \\ P=220000 \\ k=0.8036 \\ t=\text{?} \end{gathered}`

Then substitute the values into the expression

`\begin{gathered} 220000=120.7e^(0.8036t) \\ \text{Divide both sides by 120.7} \\ (220000)/(120.7)=(120.7e^(0.8036t))/(120.7) \\ \\ 1822.7009=e^(0.8036t) \\ \end{gathered}`

Take the natural logarithm of the equation in the last line

`\begin{gathered} \ln 1822.7009=\ln e^(0.8036t) \\ \ln 1822.7009=0.8036t \end{gathered}`

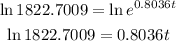
Then divide both sides by t

`\begin{gathered} (\ln 1822.7009)/(0.8036)=(0.8036t)/(0.8036) \\ (7.5081)/(0.8036)=t \\ t=9.34 \end{gathered}`

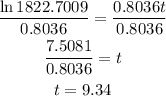
Hence

The population will reach 220000 in 9years